New parameters for the orientation of the Earth in the ICRS

Discussion extracted from Newsletter 4 of the IAU Working group T5

Nicole Capitaine

Observatoire de Paris, 3 February 2000

1. The current Earth orientation parameters

The general form of the coordinate transformation from the terrestrial reference system, TRS, to the geocentric celestial reference system, CRS, at the date t is:

\begin{displaymath}\lbrack CRS\rbrack = PN(t).R(t).W(t)\ \lbrack TRS\rbrack \,\ (1)\ \end{displaymath}

where PN(t) is the matrix transformation for the precession and nutation of the Celestial Ephemeris Pole, CEP, in the CRS, R(t) for the rotation of the Earth around the axis of the CEP and W(t) for polar motion of the CEP. We assume here that the definition of the CEP corresponds to the most accurate one (see Newsletter 3).


Until the adoption of the ICRF (Ma et al 1998), the conventional celestial frame, the FK5 based on positions and proper motions of bright stars, was oriented so that at the ``epoch'', the positions are referred to the best estimate of the location of the mean pole and mean equinox. The proper motions of stars were evaluated so that, for the adopted model of precession, they provide the best access to the mean pole and mean equinox of epoch, at any other date.

The current precession angles (see Fig 1) are those defined by Lieske et al. (1977) in the FK5 system. The current nutation angles $\Delta\psi$ in longitude and $\Delta\epsilon$ in obliquity are referred to the ecliptic of date (see Fig 1) and $\chi_A + \Delta\chi$ is the angular distance between the ecliptic of epoch and the ecliptic of date along the equator of date.

\begin{figure}\epsffile {Fk5.eps}\begin{center}{\it Figure 1 : Precession and nutation angles in the FK5 system}\end{center}\end{figure}

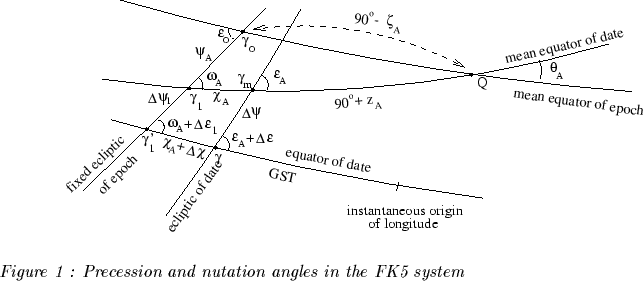
The current procedure for taking into account precession and nutation is to use the matrix transformation P(t) using the developments as function of time of the precession angles, $\zeta_A, \theta_A, z_A$, followed by the matrix transformation N(t) using the nutation angles quantities $\Delta\psi$ and $\Delta\epsilon$ provided by the conventional series of nutation (Seidelmann 1982, McCarthy 1996). Such a transformation corresponds to a sequence of six consecutive rotations for precession and nutation using five different parameters. As the precession and nutation angles are referred to the ecliptic of date, the PN(t) matrix is dependent both on the precession and nutation of the equator, due to the luni-solar and planetary torque exerted on the oblate Earth, and to precession of the ecliptic, due to planetary perturbations on the orbit of the Earth (Capitaine 1998 a, b).

The current procedure for taking into account Earth rotation in the FK5 system is to use, in the matrix R(t), the relationship between Greenwich sidereal time and UT1 (Aoki et al. 1982) giving GMST at date t, followed by the relationship between GST and GMST and then to take into account the interval of GMST from 0h UT1 to the hour of observation.

The difference GST-GMST is provided, since the 1st January 1997, by the ``complete'' equation of the equinoxes (Aoki & Kinoshita 1983, McCarthy 1996).

Additionally to Earth rotation, the angle GST thus includes (Capitaine & Gontier 1993) a part due to the accumulated precession and nutation along the equator as well as a part (in GST-GMST) due to crossed terms between precession and nutation and crossed nutation terms. It refers to the ecliptic of date and thus mixes Earth rotation and precession-nutation.

go to the top  
 

2. Proposals for new parameters

(i) Requirements for new orientation parameters

The ICRS adopted by the IAU as the International Celestial Reference System since the 1st January 1998, is defined such that the barycentric directions of distant extragalactic objects show no global rotation with respect to these objects. The fundamental properties of the ICRS is the absence of global rotation and the abandonment of the link with the motion of the Earth. The geocentric celestial reference system, designated here by CRS, follows the kinematical condition of absence of global rotation of geocentric directions of the objects realizing the ICRS.

In order to take advantage of these properties for providing the best accurate definition and measurement of Earth rotation, it is necessary to come back to more basic quantities for precession-nutation and Earth rotation, and therefore :

- to reduce the number of parameters,

- not to refer these parameters to the ecliptic of date, but to a fixed plane,

- to clearly separate the precession-nutation of the equator from the Earth rotation.


Several possibilities can be considered which use different origins on the equator.


(ii) Alternative choices for the origin on the equator

The possible choices for an origin on the moving equator are (see Fig 1, 2, 3) :

1) The true equinox, $\gamma$ which is the intersection of the moving equator with the moving ecliptic,
2) the intersection, $\gamma_1'$ of the moving equator with the fixed ecliptic,
3) the intersection, $\gamma_{xy}$ of the equator of the TRS with the equator of the CRS,
4) the intersection, K, of the zero-line meridian of the realized CRS with the moving equator,
5) The intersection, H, of the instantaneous prime meridian $P\Sigma_o$ with the moving equator,
6) The point $\Sigma$ on the moving equator such that : $\Sigma N=\Sigma_o N$,
7) The node, N, of the moving equator upon the celestial reference great circle,
8) The ``non rotating origin" (or ``departure point") on the moving equator, $\sigma$.


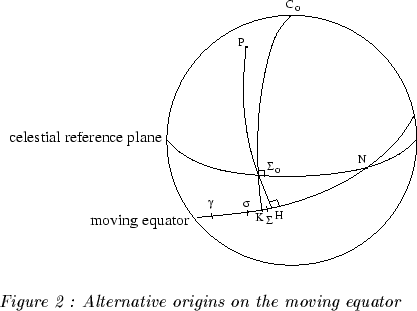
\begin{figure}\epsffile {altor.eps}\begin{center}{\it Figure 2 : Alternative origins on the moving equator}\end{center}\end{figure}

A comparison between the properties of the above definitions shows that :

- the definition 1) is dependent both on the motion of the equator and the ecliptic, whereas the other ones are dependent only on the motion of the equator,

- the definition 2) is on the fixed equator of the TRS, whereas the other ones are on the moving equator,

- the definitions 2) to 7) have geometrical meaning, whereas the definition 8) has a kinematical meaning (Guinot 1979).


(iii) Euler's angles

The classical representation using Euler's angles (Fig 3) between the terrestial frame, TRS=[Oxyz] and the celestial frame, [OXYZ], as used by Woolard (1953) refers to the ecliptic frame at epoch, which can easily be transformed to the mean equatorial frame at epoch taking into account the obliquity of the ecliptic ($\epsilon_0$) at epoch and then transformed to the ICRS, taking into account the offsets between this frame and the CRS. We will consider here that CRS=[OXYZ].

\begin{figure}\vspace*{-0.3cm}\epsffile {Euler.eps}\begin{center}{\it Figure 3......TRS and the CRS and the Earth'srotation} $\vec{\omega}$\end{center}\end{figure}

The transformation matrix from the TRS to the CRS is based upon three parameters, the origin for the angle $\phi$ being $\gamma_{xy}$ as defined by (3) on the equator of the TRS.

The two first angles, ($\theta$ and $\psi$), include both polar motion and precession-nutation referred to the ecliptic of epoch and the third one, $\phi$, include both Earth rotation and the motion of $\gamma_{xy}$, due to precession-nutation of the equator of figure.

No intermediate pole is used in such a transformation between the TRS and the CRS and the transformation matrix between the TRS and CRS is :

\begin{displaymath}\lbrack CRS\rbrack = R_3(-\psi).R_2(-\theta).R_3(-\phi)\ \lbrack TRS\rbrack\,\ (2)\ \end{displaymath}

When the considered celestial frame is the ecliptic frame at J2000, the solutions for the precession-nutation part of the Euler's angles are provided, at a microarsecond accuracy, for a rigid Earth by Bretagnon et al. 1997.


(iv) Combined precession and nutation parameters

(i) : Aoki & Kinoshita (1983) have considered a combined form of three rotations from the ecliptic frame of epoch (see Fig 1) :

\begin{displaymath}PN(t) =R_3(\psi_A+\Delta\psi_1).R_1(\omega_{A}+\Delta\epsilon_1).R_3(-\chi-\Delta\chi)\ ,\ (3)\end{displaymath}

using the parameters $\psi_A+\Delta\psi_1$ and $\epsilon_1+\Delta\epsilon_1$ which include precession and nutation referred to the fixed ecliptic (see Fig 1), and can thus be easily referred to the fixed equator and then to the ICRS.

Such parameters are supposed to refer to an intermediate pole such as the CEP.

In the case where only the two last parameters are considered, $\psi_A+\Delta\psi_1,\omega_{A}+\Delta\epsilon_1$, the corresponding origin on the equator is $\gamma_1'$ as given by the definition 2), whereas if the three parameters are considered, the origin is the current true equinox $\gamma$.

That corresponds to six and seven parameters respectively for the whole transformation from the TRS to the CRS.


(v) The coordinates of the CEP in the CRS and the TRS

The celestial pole coordinates $X, Y$ (Fig 4) (or direction cosines) of the CEP in the CRS (Capitaine 1990) include precession, nutation, the coupling effects between precession and nutation, crossed-nutation terms and the offsets of the precession-nutation models at J2000.0 wrt the pole of the ICRF.

\begin{figure}\epsffile {CoordXY.eps}\begin{center}{\it Figure 4 : The coordina......of the pole P in the CRS andthe TRS (Capitaine 1990)}\end{center}\end{figure}

They can be related to the current quantities for precession and nutation by :

\begin{eqnarray*}X =\sin d\cos E&=&\chi_{o} + \sin (\omega_{A}+ \Delta \epsilon......\Delta \epsilon _{1}) \cos (\psi_{A}+ \Delta \psi _{1})\ ,\ (4)\end{eqnarray*}



$\chi_{o} , \eta_{o}$ being the celestial offsets between the computed pole at J2000.0 and the pole of the ICRS.

The matrix transformation taking into account X and Y is :

\begin{displaymath}PN(t)=R_3(-E).R_2(-d).R_3(E)\ .\ \\ (5)\end{displaymath}

Development as function of time of $X$ and $Y$ at a microarsecond accuracy after one century are provided by Capitaine et al.(1999) in consistency with the IERS 1996 precession and nutation and the numerical values (IERS Annual Report for 1997) of the celestial offsets at J2000.0. Such developments (Table 1a and Table 1b) include a constant term, a polynomial form of t, a sum of periodic terms and a sum of Poisson terms.

These parameters are supposed to be referred to an intermediate pole, such as the CEP, and appears in a symmetric form as the coordinates in the TRS, $x_p=\sin g\cos F$, $y_p=\sin g\sin F$ (Fig 4), which can be taken into account by the matrix transformation :

\begin{displaymath}W(t)=R_3(-F).R_2(g).R_3(F)\ .\ \\ (6)\end{displaymath}

Such a transformation corresponds to five parameters for the whole transformation from the CRS to the TRS and the corresponding geometric origin on the true equator is the point $\Sigma$ as given by the definition 6).

These parameters, $X$, $Y$ of the CEP in the CRS and $x_p, y_p$ the ``polar motion'' in the TRS are also those adopted by Mathews (1999 b) who takes into account Earth rotation by the angle $\chi$ on the moving equator. This angle, due to its realization by the transformation matrix from the TRS to the CRS, is reckoned from the point $\Sigma$.


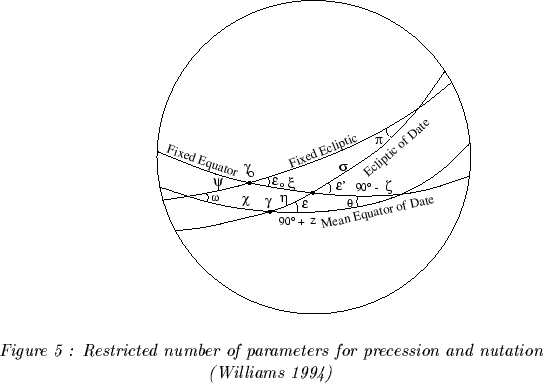
(vi) Restricted number of parameters for precession-nutation

Williams (1994) has proposed a restricted number of parameters in order to minimize the number of rotations when combining the rotations for precession and nutation. The subscript A is not used with symbols in the figure (Fig 5) and the obliquity of the ecliptic, precession in longitude along the ecliptic of date and planetary precession along the fixed equator are considered as including both precession and nutation. Such a transformation can be written when introducing explicitly the nutation as :

\begin{displaymath}PN(t)=R_3(-\xi).R_1(-\epsilon').R_3(\eta+\Delta\psi).R_1(\epsilon+\Delta\epsilon)\ (7)\end{displaymath}

This is similar to (3), but with the disadvantage that the considered parameters $\eta+\Delta\psi$ and $\epsilon+\Delta\epsilon$ are here referred to the ecliptic of date, the origin on the moving equator being the true equinox $\gamma$.

\begin{figure}\epsffile {Obl.eps}\begin{center}{\it Figure 5 : Restricted numbe......arameters for precession and nutation(Williams 1994)}\end{center}\end{figure}


(vii) Celestial and terrestrial coordinates of the pole of angular momentum axis

The variables adopted by Fukujima (1994) are the magnitude components of the angular momentum vector in the CRS (XYZ) and in the TRS (ABC) and the longitude of $A$-axis measured from $X$-axis along the great circle perpendicular to the angular momentum of date.

The orientation matrix from the TRS to the CRS is thus generated by five successive rotations.

These variables (very similar to (v) are referred to the axis of angular momentum and it can be shown that the corresponding origin on the moving equator is the point K as defined by 4), but relative to the plane perpendicular to the angular momentum axis.


(viii) The celestial coordinates of the pole of the TRS

Other parameters $X'$ and $Y'$ can be defined by including polar motion as high frequency variations in the celestial pole coordinates $X$ and $Y$ as defined in (v). In that case, there is no intermediate axis and the parameters are then referred to the z-axis of the TRS.

The corresponding angles $90°+E$ and $d$ would then be similar to the two first Euler angles between the TRS and the CRS.

The origin on the equator of the TRS can be defined in a similar way as the origin $\Sigma$ as defined by 6).


(ix) The Earth's angle of rotation

The Earth's angle of rotation as reckoned from any geometrical origin inevitably includes, additionally to Earth rotation, the accumulated rotation of this origin wrt the CRS along the moving equator due to the precession-nutation of the equator. This is the case for all the origins considered in sections (iii) to (viii).

For defining an Earth's angle of rotation which includes only the ``intrinsic Earth rotation'', it is necessary to eliminate the spurious rotation of the origin on the moving equator.

It is thus necessary to use an origin defined by the kinematical property of having ``no instantaneous rotation'' around the axis of rotation wrt the CRS. That provides the ``non rotating origin" $\sigma$ (Guinot 1979), which can be designated as ``the Celestial Ephemeris Origin'' (CEO) when referred to the axis of the CEP.

The ``stellar angle'' is defined by $\theta=\varpi \sigma$ (see Fig 6) and is such that $\dot{\theta}=\omega_3$ (the component of the angular velocity vector along the axis of the CEP) and thus $\theta$ includes only Earth rotation.

\begin{figure}\epsffile {Deftheta.eps}\begin{center}{\it Figure 6 : Definition of the stellar angle $\theta$}\end{center}\end{figure}

The quantity $s$, which is the angular distance of $\sigma$ to $\Sigma$ must be included in the PN(t) matrix as it originates from precession and nutation. A similar quantity $s$', which is the angular distance of $\sigma$ to $\varpi$ (the instantaneous origin of the longitudes on the moving equator) has to be included in the $W(t)$ matrix as it originates from polar motion.

The numerical development of $s$ and $s'$ compatible with the IERS Conventions 1996 is provided by Capitaine et al. (1999).


(x) Comparison between the different options

A comparison of the parameters considered above shows that Euler's angles (described in (iii)) or equivalently the celestial coordinates of the z-axis of the TRS (described in (viii)), which reduce to three the number of EOP, do not use any intermediate pole and consequently include both high frequency and low frequency components of the motion of the z-axis of the TRS wrt the CRS.

The other parameters separate the celestial components from the terrestrial components according to a ``frequency criteria'' using an intermediate pole. Such a procedure facilitates the estimation of the parameters from observations, unless the model for low frequency motion in space is perfect.

The difference between the use of a geometrical origin (as $\Sigma$ or $K$ for examples) and a kinematical origin ($\sigma$) is that, in the first case, the instantaneous rotation of the considered origin is included in the derived value for the Earth's angle rotation, whereas it is clearly separated when using directly $\sigma$ as the origin on the moving equator.


References

Aoki, S., Guinot, B., Kaplan, G. H., Kinoshita, H., McCarthy, D. D., Seidelmann, P. K., 1982, Astron. Astrophys. 105, 359.

Aoki, S. and Kinoshita 1983, Celest. Mech., 29, pp. 335-360.

Bretagnon P., Rocher P., and Simon J.-L., 1997, Astron. Astrophys. 319, pp 305-317.

Capitaine, N., 1998 a, in Highlights of Astronomy, 11A, 153-157.

Capitaine, N., 1998 b, in the Proceedings of the Journées Systèmes de Référence Spatio-Temporels 1997, J. Vondrak and N. Capitaine, eds, pp 83-86.

Capitaine, N., 1990, Celest. Mech. Dyn. Astr. 48, pp. 127-143.

Capitaine, N., Gontier, A.M., 1993, Astron. Astrophys. 275, 645-650.

Capitaine, N., Guinot, B., McCarthy, D.D., 1999, Astron. Astrophys. 105, in press.

Fukujima, T., 1996, Astron. J., 112 (3), pp. 1263-1277.

Guinot, B., 1979, in Time and the Earth's Rotation, D.D. Mc Carthy, J.D. Pilkington (eds), D. Reidel Publishing Company, 7.

Lieske, J. H., Lederle, T., Fricke, W., and Morando, B., 1977, Astron. Astrophys. 58, 1.

Ma, C.,Arias, E.F., Eubaks, M. Fey, A.L., Gontier, A.-M., Jacobs, C.S., Archninal, B.A., Charlot, P., 1998, Astron. J., 116, pp. 516-546.

Mathews, P.M., 1999 b, in the Proceedings of the Journées Systèmes de Référence Spatio-Temporels 1998, N. Capitaine ed, Observatoire de Paris, pp 69-70.

McCarthy D.D., 1996, ``IERS Conventions'', IERS Technical Note 21, Observatoire de Paris.

Seidelmann, P. K., 1982, Celest. Mech., 27, pp. 79-106.

Williams J.G., 1994, Astron. J., 108, pp. 711-724.

Woolard, E. W., 1953, Astr. Pap. Amer. Ephem. Naut. Almanach XV, I, 1-165.

go to the top    

3. Questions to the subgroup T5


(1) Do you agree that the current parameters in the FK5 system must be abandoned for being consistent with the newly adopted ICRS ?


(2) Do you agree that, for consistency with ICRS, the current formulation combining the motions of the equator and of the ecliptic wrt the CRS has to be abandoned ?


(3) Do you agree that the angle of Earth rotation must no more be reckoned from the true equinox which is moving due to precession and nutation and which is referred to the ecliptic of date ?


(4) Do you agree that new parameters for the orientation of the Earth's axis in the CRS must include both precession and nutation ?


(5) Which parameters (either among the parameters presented previously or new ones) do you propose to use for the EOP referred to the ICRS in place of the current parameters referred to the FK5 ?


(6) Which origin on the moving equator do you prefer ?


(7) Do you agree that in order to provide Earth rotation form the orientation angle around the axis of the CEP, it is necessary to use an origin without any instantaneous rotation wrt the CRS around this axis ?

go to the top