1. The current Earth orientation parameters

The general form of the coordinate transformation from the terrestrial reference system, TRS, to the geocentric celestial reference system, CRS, at the date t is:

$$\lbrack CRS\rbrack = PN(t).R(t).W(t)\ \lbrack TRS\rbrack \,\ (1)\$$

where PN(t) is the matrix transformation for the precession and nutation of the Celestial Ephemeris Pole, CEP, in the CRS, R(t) for the rotation of the Earth around the axis of the CEP and W(t) for polar motion of the CEP. We assume here that the definition of the CEP corresponds to the most accurate one (see Newsletter 3).

Until the adoption of the ICRF (Ma et al 1998), the conventional celestial frame, the FK5 based on positions and proper motions of bright stars, was oriented so that at the ``epoch'', the positions are referred to the best estimate of the location of the mean pole and mean equinox. The proper motions of stars were evaluated so that, for the adopted model of precession, they provide the best access to the mean pole and mean equinox of epoch, at any other date.

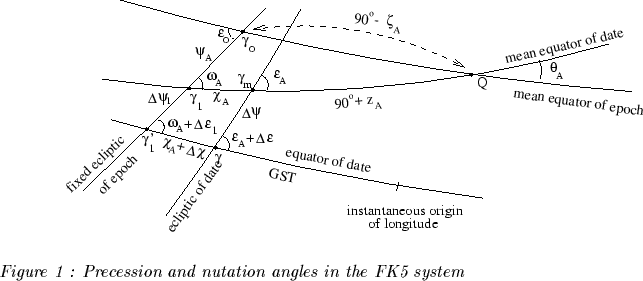
The current precession angles (see Fig 1) are those defined by Lieske et al. (1977) in the FK5 system. The current nutation angles $\Delta\psi$ in longitude and $\Delta\epsilon$ in obliquity are referred to the ecliptic of date (see Fig 1) and $\chi_A + \Delta\chi$ is the angular distance between the ecliptic of epoch and the ecliptic of date along the equator of date.

The current procedure for taking into account precession and nutation is to use the matrix transformation P(t) using the developments as function of time of the precession angles, $\zeta_A, \theta_A, z_A$, followed by the matrix transformation N(t) using the nutation angles quantities $\Delta\psi$ and $\Delta\epsilon$ provided by the conventional series of nutation (Seidelmann 1982, McCarthy 1996). Such a transformation corresponds to a sequence of six consecutive rotations for precession and nutation using five different parameters. As the precession and nutation angles are referred to the ecliptic of date, the PN(t) matrix is dependent both on the precession and nutation of the equator, due to the luni-solar and planetary torque exerted on the oblate Earth, and to precession of the ecliptic, due to planetary perturbations on the orbit of the Earth (Capitaine 1998 a, b).

The current procedure for taking into account Earth rotation in the FK5 system is to use, in the matrix R(t), the relationship between Greenwich sidereal time and UT1 (Aoki et al. 1982) giving GMST at date t, followed by the relationship between GST and GMST and then to take into account the interval of GMST from 0h UT1 to the hour of observation.

The difference GST-GMST is provided, since the 1st January 1997, by the ``complete'' equation of the equinoxes (Aoki & Kinoshita 1983, McCarthy 1996).

Additionally to Earth rotation, the angle GST thus includes (Capitaine & Gontier 1993) a part due to the accumulated precession and nutation along the equator as well as a part (in GST-GMST) due to crossed terms between precession and nutation and crossed nutation terms. It refers to the ecliptic of date and thus mixes Earth rotation and precession-nutation.