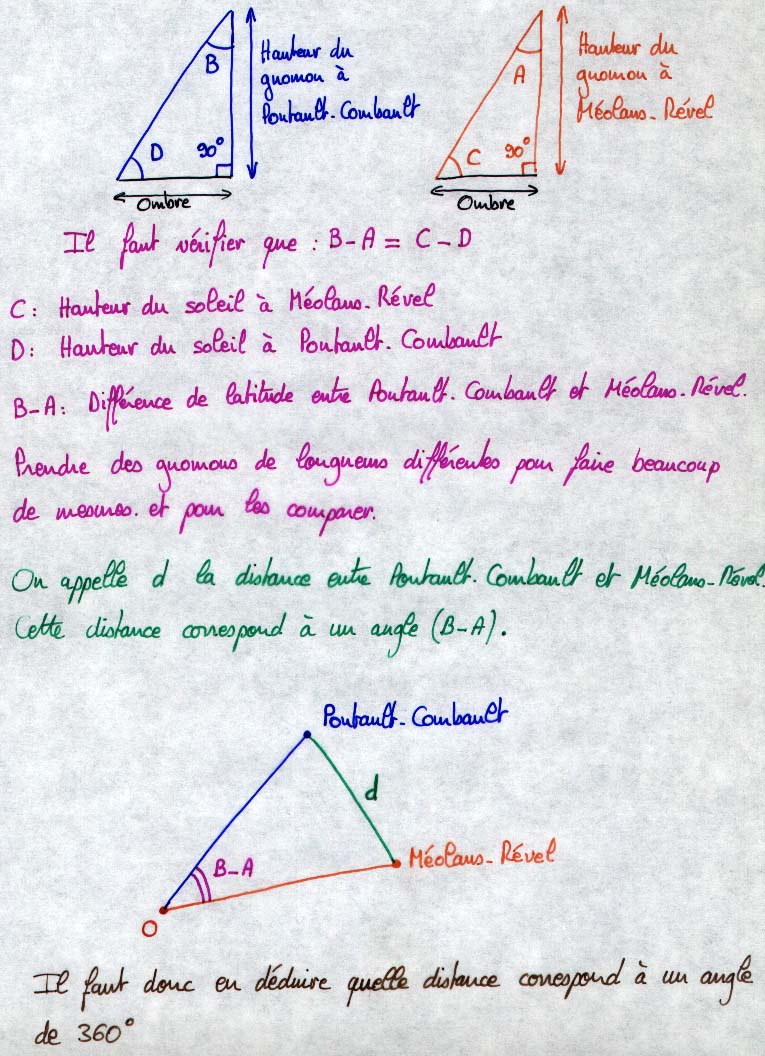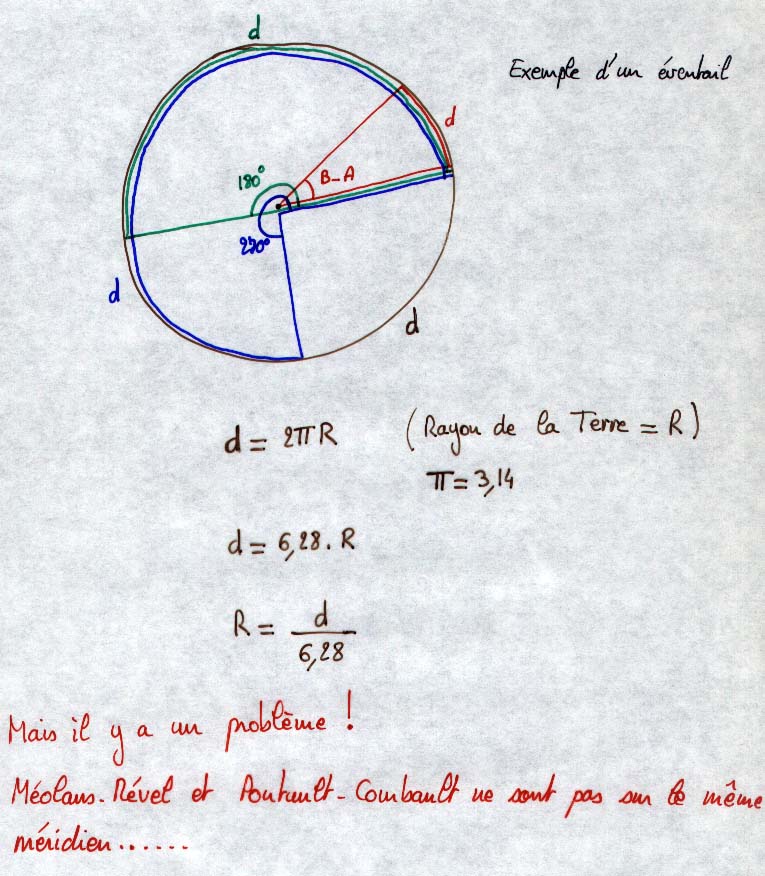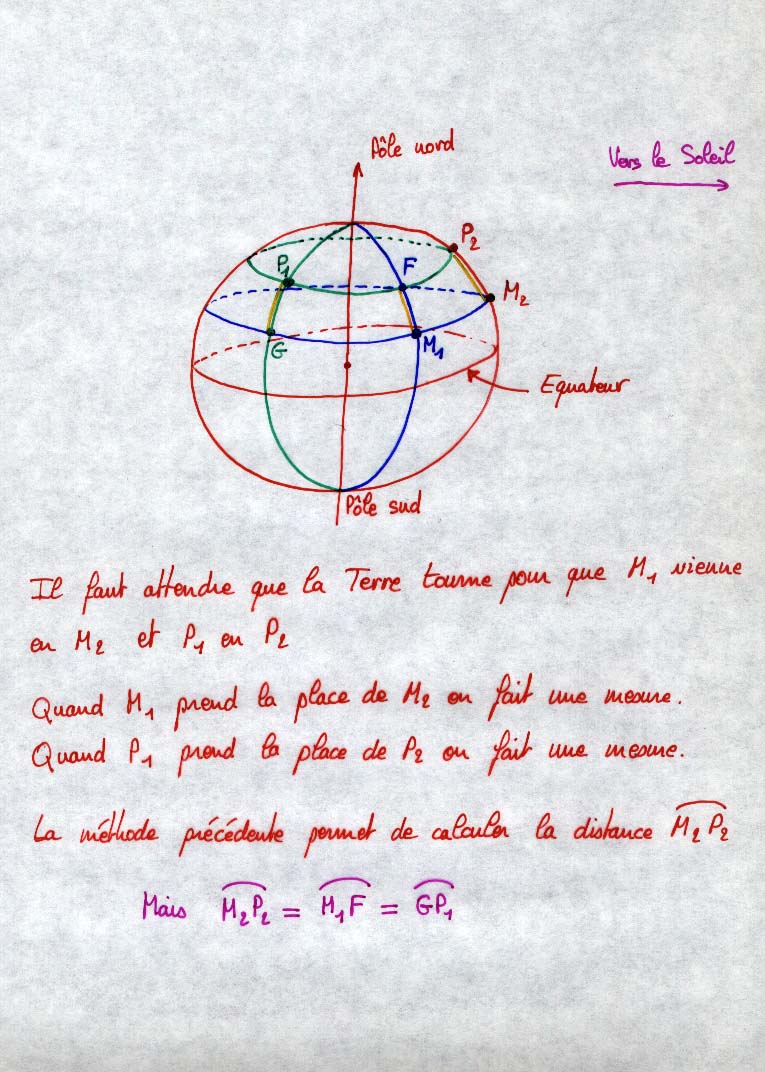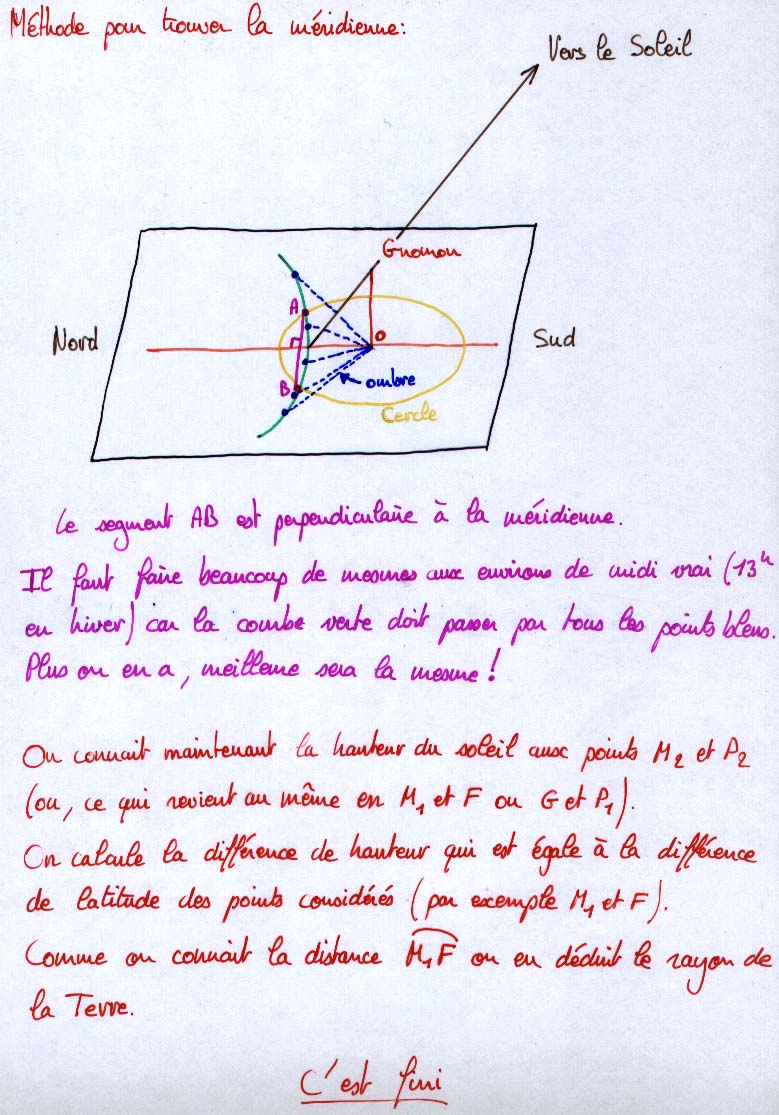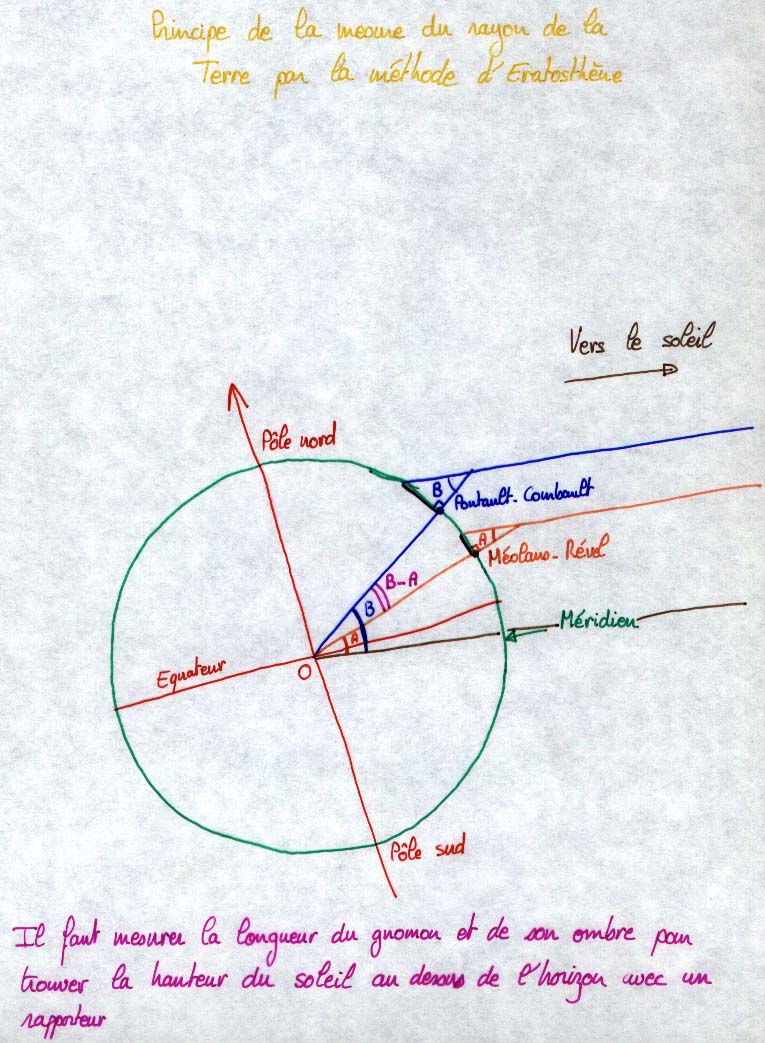
Transparent n°1: Principe de la méthode d'Eratosthène dans le cas de Pontault-Combault et de Méolans-Rével. Ce graphique représente les deux villes situées sur le même méridien ce qui n'est pas la cas dans la réalité. La vérité sera rétablie un peu plus loin... Le principe est de mesurer l'angle noté (B-A) qui est égal à la différence des hauteurs du soleil dans les deux villes. Connaissant la distance entre Pontault et Méolans (mesurée sur une carte) on en déduit le périmètre de la Terre et donc sont rayon

 

Transparent n°2: On montre ici que la différence de hauteurs du soleil est égale à la différence de latitude des deux villes. Pour vérifier l'égalité B-A=C-D on peut utiliser des triangles découpés dans du carton. Les mesures de hauteurs peuvent avantageusement être multipliées (effectuées par plusieurs groupes d'enfants avec des gnomons de longueurs différentes) afin d'effectuer des moyennes. La figure du bas montre la relation entre l'angle B-A déduit des mesures sur le terrain et la distance des deux villes mesurées sur une carte.

 

Transparent n°3: L'exemple d'un éventail qui s'ouvre progressivement peut permettre aux enfants de comprendre la relation de proportionnalité qui existe entre l'angle et la longueur de l'arc de cercle correspondant. Des mesures peuvent au besoin être effectuées sur un véritable éventail à l'aide d'une ficelle tout comme la relation liant le périmètre du cercle à son rayon peut être découverte (possibilité de recherches historiques sur le nombre pi, quand, comment et par qui la relation en question a-t-elle été découverte...). Une fois connu le périmètre de la Terre son rayon s'en déduit très facilement. On en arrive maintenant au moment ou il faut expliquer aux enfants que Méolans et Pontault ne sont pas sur le même méridien... Pour visualiser le problème une carte de France ou un globe terrestre peuvent être utilisés avec profit.

 

Transparent n°4: Afin de se ramener dans la situation du transparent n°1 il suffit d'attendre que la Terre tourne d'un angle correspondant à la différence de longitude entre Pontault et Méolans. Le point Pontault-Combault du transparent n°1 correspond au point P2 du transparent n°4 et le point Méolans correspond au point M2 (ces points sont atteints avec un décalage temporel correspondant à la différence de longitudes). Sur le dessin le soleil se trouve dans le plan passant par l'axe des pôles et les points P2 ou M2. On mesure donc la distance M2P2 ou M1F ou GP1 ou toutes distances entre les points situés sur les parallèles passant par Pontault et Méolans.

 

Transparent n°5:

 

Transparent n°6: L'instant de passage d'un astre au méridien d'un lieu se produit lorsque la hauteur de cet astre au dessus de l'horizon est maximum. Dans le cas du soleil cet instant peut être facilement mesuré puisque la longueur de l'ombre d'un gnomon est à cet instant minimum. Le dessin ci-contre montre la longueur de l'ombre en fonction de la hauteur du soleil au dessus de l'horizon.

 

Transparent n°7: Pour déterminer la méridienne du lieu (trace du plan du méridien au sol) on repère la position de l'ombre d'un gnomon en fonction de l'heure de la journée (par exemple toutes les heures à partir de 9h le matin jusqu'à 16h l'après-midi). On obtient en général un arc d'hyperbole (une droite aux équinoxes). On trace ensuite un cercle de centre le pied du gnomon et de rayon tel que ce cercle puisse intercepter la courbe en deux points. On trace la droite qui passe par ces deux points. La médiatrice du segment délimité par les deux points d'intersection entre le cercle et la droite est la méridienne du lieu. La méridienne est aussi la droite qui passe par le pied du gnomon et par le milieu du segment précédent.