IAU RESOLUTIONS
ADOPTED THE 24th GENERAL ASSEMBLY
(Manchester, August 2000)
Final version of resolutions
English - Word doc
English - Word rtf
English-Postcript
French-Postcript
Resolution B1.1 Maintenance and
Establishment of Reference Frames and Systems
The XXIVth International Astronomical Union General
Assembly,
Noting
-
that Resolution B2 of the XXIIIrd General Assembly
(1997) specifies that "the fundamental reference frame shall be the International
Celestial Reference Frame (ICRF) constructed by the IAU Working Group on
Reference Frames,"
-
that Resolution B2 of the XXIIIrd General Assembly
(1997) specifies "That the Hipparcos Catalogue shall be the primary realisation
of the International Celestial Reference System (ICRS) at optical wavelengths",
and
-
the need for accurate definition of reference systems
brought about by unprecedented precision, and
Recognising
-
the importance of continuing operational observations
made with Very Long Baseline Interferometry (VLBI) to maintain the ICRF,
-
the importance of VLBI observations to the operational
determination of the parameters needed to specify the time-variable transformation
between the International Celestial and Terrestrial Reference Frames,
-
the progressive shift between the Hipparcos frame
and the ICRF, and
-
the need to maintain the optical realisation as close
as possible to the ICRF
Recommends
-
that IAU Division I maintain the Working Group on
Celestial Reference Systems formed from Division I members to consult with
the International Earth Rotation Service (IERS) regarding the maintenance
of the ICRS,
-
that the IAU recognise the International VLBI service
(IVS) for Geodesy and Astrometry as an IAU Service Organization,
-
that an official representative of the IVS be invited
to participate in the IAU Working Group on Celestial Reference Systems,
-
that the IAU continue to provide an official representative
to the IVS Directing Board,
-
that the astrometric and geodetic VLBI observing
programs consider the requirements for maintenance of the ICRF and linking
to the Hipparcos optical frame in the selection of sources to be observed
(with emphasis on the Southern Hemisphere), design of observing networks,
and the distribution of data, and
-
that the scientific community continue with high
priority ground- and space-based observations (a) for the maintenance of
the optical Hipparcos frame and frames at other wavelengths and (b) for
links of the frames to the ICRF.
Resolution B1.2 Hipparcos
Celestial Reference Frame
The XXIVth International Astronomical Union General
Assembly,
Noting
-
that Resolution B2 of the XXIIIrd General Assembly
(1997) specifies, "That the Hipparcos Catalogue shall be the primary realisation
of the International Celestial Reference System (ICRS) at optical wavelengths;",
-
the need for this realisation to be of the highest
precision,
-
that the proper motions of many of the Hipparcos
stars known, or suspected, to be multiple are adversely affected by uncorrected
orbital motion,
-
the extensive use of the Hipparcos Catalogue as reference
for the ICRS in extension to fainter stars,
-
the need to avoid confusion between the International
Celestial Reference Frame (ICRF) and the Hipparcos frame, and
-
the progressive shift between the Hipparcos frame
and the ICRF,
Recommends
-
that Resolution B2 of the XXIIIrd IAU General Assembly
(1997) be amended by excluding from the optical realisation of the ICRS
all stars flagged C, G, O, V and X in the Hipparcos Catalogue, and
-
that this modified Hipparcos frame be labelled the
Hipparcos Celestial Reference Frame (HCRF).
Resolution B1.3 Definition
of Barycentric Celestial Reference System and Geocentric Celestial Reference
System
The XXIVth International Astronomical Union General
Assembly,
Considering
-
that the Resolution A4 of the XXIst General Assembly
(1991) has defined a system of space-time coordinates for (a) the solar
system (now called the Barycentric Celestial Reference System, (BCRS))
and (b) the Earth (now called the Geocentric Celestial Reference System
(GCRS)), within the framework of General Relativity,
-
the desire to write the metric tensors both in the
BCRS and in the GCRS in a compact and self-consistent form,
-
the fact that considerable work in General Relativity
has been done using the harmonic gauge that was found to be a useful and
simplifying gauge for many kinds of applications,
Recommends
-
the choice of harmonic coordinates both for the barycentric
and for the geocentric reference systems,
-
writing the time-time component and the space-space
component of the barycentric metric gm
nwith barycentric coordinates (t,
x) (t = Barycentric Coordinate Time (TCB)) with a single scalar potential
w(t, x) that generalises the Newtonian potential, and the space-time
component with a vector potential wi(t, x); as a boundary
condition it is assumed that these two potentials vanish far from the solar
system,
explicitly,
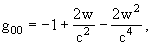
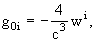
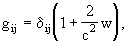
with
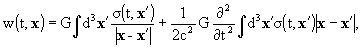
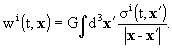
here, s and si
are the gravitational mass and current densities, respectively,
-
writing the geocentric metric tensor Gab
with geocentric coordinates (T, X) (T= Geocentric Coordinate Time
(TCG)) in the same form as the barycentric one but with potentials W(T,
X) and Wa(T,
X); these geocentric potentials should
be split into two parts - potentials WE and
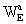 arising
from the gravitational action of the Earth and external parts
arising
from the gravitational action of the Earth and external parts 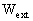 and
and 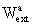 due
to tidal and inertial effects; the external parts of the metric potentials
are assumed to vanish at the geocenter and admit an expansion into positive
powers of X,
due
to tidal and inertial effects; the external parts of the metric potentials
are assumed to vanish at the geocenter and admit an expansion into positive
powers of X,
explicitly,
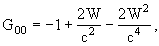
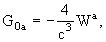
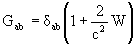 ,
,
the potentials W and Wa should be split
according to
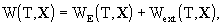
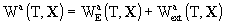 ,
,
the Earth's potentials WE and 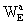 are
defined in the same way as w and wi but with quantities calculated
in the GCRS with integrals taken over the whole Earth,
are
defined in the same way as w and wi but with quantities calculated
in the GCRS with integrals taken over the whole Earth,
-
using, if accuracy requires, the full post-Newtonian
coordinate transformation between the BCRS and the GCRS as induced by the
form of the corresponding metric tensors,
explicitly, for the kinematically non-rotating
GCRS (T=TCG, t=TCB, 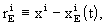 and
a summation from 1 to 3 over equal indices is
implied),
and
a summation from 1 to 3 over equal indices is
implied),
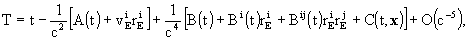
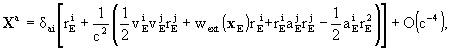
where
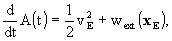
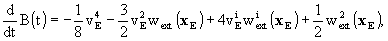
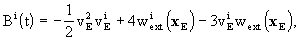
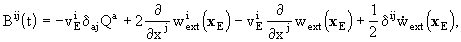
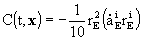 ,
,
here 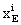 ,
, 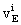 ,
and
,
and 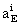 are the components of
the barycentric position, velocity and acceleration vectors of the Earth,
the dot stands for the total derivative with respect to t, and
are the components of
the barycentric position, velocity and acceleration vectors of the Earth,
the dot stands for the total derivative with respect to t, and
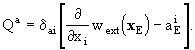
The external potentials, 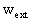 and
and 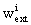 ,
are given by
,
are given by
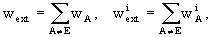 where E stands for the Earth and wAand
where E stands for the Earth and wAand 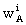 are
determined by the expressions for w and
are
determined by the expressions for w and 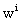 with
integrals taken over body A only.
Notes
with
integrals taken over body A only.
Notes
It is to be understood that these expressions
for w and wi give g00 correct
up to O(c-5), g0i up to O(c-5),
and gij up to O(c-4). The densities
s and si
are determined by the components of the energy momentum tensor of the matter
composing the solar system bodies as given in the references. Accuracies
for Gab in terms of c-n correspond to those
of gm n .
The external potentials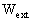 and
and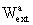 can
be written in the form
can
be written in the form

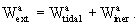
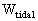 generalises
the Newtonian expression for the tidal potential. Post-Newtonian expressions
for
generalises
the Newtonian expression for the tidal potential. Post-Newtonian expressions
for 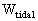 and
and 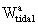 can
be found in the references. The potentials
can
be found in the references. The potentials 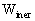 ,
, 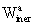 are
inertial contributions that are linear in
are
inertial contributions that are linear in 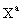 .
The former is determined mainly by the coupling of the Earth's nonsphericity
to the external potential. In the kinematically non-rotating Geocentric
Celestial Reference System,
.
The former is determined mainly by the coupling of the Earth's nonsphericity
to the external potential. In the kinematically non-rotating Geocentric
Celestial Reference System, 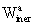 describes
the Coriolis force induced mainly by geodetic precession.
describes
the Coriolis force induced mainly by geodetic precession.
Finally, the local gravitational potentials 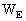 and
and 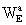 of
the Earth are related to the barycentric gravitational potentials
of
the Earth are related to the barycentric gravitational potentials 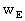 and
and 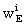 by
by
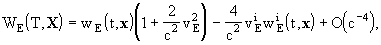
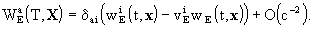
References
Brumberg, V.A., Kopeikin, S.M., 1988, Nuovo
Cimento B 103, 63.
Brumberg, V.A., 1991, Essential Relativistic
Celestial Mechanics, Hilger, Bristol.
Damour, T., Soffel, M., Xu, C., Phys.Rev. D
43, 3273 (1991);
45, 1017 (1992); 47, 3124 (1993);
49, 618 (1994).
Klioner, S. A., Voinov, A.V., 1993, Phys Rev.
D, 48, 1451.
Kopeikin, S.M., 1989, Celest. Mech., 44,
87.
Resolution B1.4 Post-Newtonian
Potential Coefficients
The XXIVth International Astronomical Union General
Assembly,
Considering
-
that for many applications in the fields of celestial
mechanics and astrometry a suitable parametrization of the metric potentials
(or multipole moments) outside the massive solar system bodies in the form
of expansions in terms of potential coefficients are extremely useful,
and
-
that physically meaningful post-Newtonian potential
coefficients can be derived from the literature,
Recommends
-
expansion of the post-Newtonian potential of the
Earth in the Geocentric Celestial Reference System (GCRS) outside the Earth
in the form
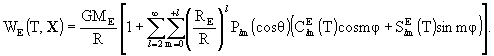
here 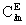 and
and 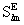 are,
to sufficient accuracy, equivalent to the post-Newtonian multipole moments
introduced by Damour et al. (Damour et al., Phys. Rev.
D, 43, 3273, 1991). q and f
are the polar angles corresponding to the spatial coordinates
are,
to sufficient accuracy, equivalent to the post-Newtonian multipole moments
introduced by Damour et al. (Damour et al., Phys. Rev.
D, 43, 3273, 1991). q and f
are the polar angles corresponding to the spatial coordinates 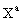 of
the GCRS and
of
the GCRS and 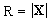 , and
, and
-
expression of the vector potential outside the Earth,
leading to the well-known Lense-Thirring effect, in terms of the Earth's
total angular momentum vector
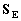
in the form
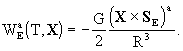
Resolution B1.5 Extended relativistic
framework for time transformations and realisation of coordinate times
in the solar system
The XXIVth International Astronomical Union General
Assembly,
Considering
-
that the Resolution A4 of the XXIst General Assembly
(1991) has defined systems of space-time coordinates for the solar system
(Barycentric Reference System) and for the Earth (Geocentric Reference
System), within the framework of General Relativity,
-
that Resolution B1.3 entitled "Definition of Barycentric
Celestial Reference System and Geocentric Celestial Reference System" has
renamed these systems the Barycentric Celestial Reference System (BCRS)
and the Geocentric Celestial Reference System (GCRS), respectively, and
has specified a general framework for expressing their metric tensor and
defining coordinate transformations at the first post-Newtonian level,
-
that, based on the anticipated performance of atomic
clocks, future time and frequency measurements will require practical application
of this framework in the BCRS,
-
that theoretical work requiring such expansions has
already been performed,
Recommends
that for applications that concern time transformations
and realisation of coordinate times within the solar system, Resolution
B1.3 be applied as follows:
-
the metric tensor be expressed as
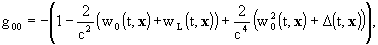
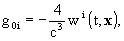
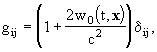
where (t º Barycentric
Coordinate Time (TCB), x) are the barycentric coordinates, 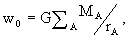 with
the summation carried out over all solar system bodies A, rA
= x - xA , xA are the coordinates
of the center of mass of body A, rA = |rA|,
and where wL contains the expansion in terms of multipole moments
[see their definition in the Resolution B1.4 entitled "Post-Newtonian Potential
Coefficients"] required for each body. The vector potential
with
the summation carried out over all solar system bodies A, rA
= x - xA , xA are the coordinates
of the center of mass of body A, rA = |rA|,
and where wL contains the expansion in terms of multipole moments
[see their definition in the Resolution B1.4 entitled "Post-Newtonian Potential
Coefficients"] required for each body. The vector potential 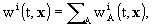 and
the function
and
the function 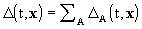 are given
in note 2.
are given
in note 2.
-
the relation between TCB and Geocentric Coordinate
Time (TCG) can be expressed to sufficient accuracy by
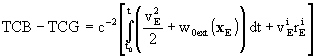
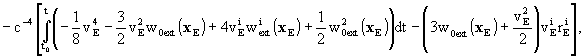 where vE is the barycentric velocity
of the Earth and where the index ext refers to summation over all bodies
except the Earth.
Notes
where vE is the barycentric velocity
of the Earth and where the index ext refers to summation over all bodies
except the Earth.
Notes
1. This formulation will provide an uncertainty
not larger than 5 x 10-18 in rate and, for quasi-periodic
terms, not larger than 5 x 10-18 in rate amplitude and
0.2 ps in phase amplitude, for locations farther than a few solar radii
from the Sun. The same uncertainty also applies to the transformation between
TCB and TCG for locations within 50000 km of the Earth. Uncertainties in
the values of astronomical quantities may induce larger errors in the formulas.
2. Within the above mentioned uncertainties,
it is sufficient to express the vector potential 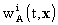 of
body A as
of
body A as
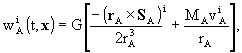 where SA is the total angular
momentum of body A and
where SA is the total angular
momentum of body A and 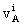 are
the components of the barycentric coordinate velocity of body A. As for
the function
are
the components of the barycentric coordinate velocity of body A. As for
the function 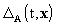 it is sufficient
to express it as
it is sufficient
to express it as
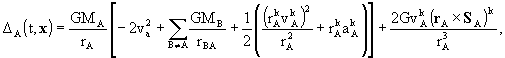
where 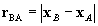 and
and 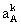 is
the barycentric coordinate acceleration of body A. In these formulas, the
terms in SA are needed only for Jupiter (S »
6.9´ 1038 m2s-1kg)
and Saturn (S » 1.4´
1038 m2s-1kg), in the immediate vicinity
of these planets.
is
the barycentric coordinate acceleration of body A. In these formulas, the
terms in SA are needed only for Jupiter (S »
6.9´ 1038 m2s-1kg)
and Saturn (S » 1.4´
1038 m2s-1kg), in the immediate vicinity
of these planets.
3. Because the present Recommendation provides
an extension of the IAU 1991 recommendations valid at the full first post-Newtonian
level, the constants LC and LB that were introduced
in the IAU 1991 recommendations should be defined as <TCG/TCB> = 1 -
LC and <TT/TCB> = 1 - LB , where TT refers to
Terrestrial Time and <> refers to a sufficiently long average taken
at the geocenter. The most recent estimate of LC is (Irwin,
A. and Fukushima, T., 1999, Astron. Astroph. 348, 642-652)
LC = 1.48082686741´
10-8 ± 2´
10-17,
From the Resolution B1.9 on "Redefinition of
Terrestrial Time TT", one infers LB
= 1.55051976772 ´ 10-8 ±
2´ 10-17 by using the relation
1-LB=(1-LC)(1-LG).
LG
is defined in Resolution B1.9.
Because no unambiguous definition may be provided
for LB and LC , these constants should
not be used in formulating time transformations when it would require knowing
their value with an uncertainty of order 1´
10-16 or less.
4. If TCB-TCG is computed using planetary ephemerides
which are expressed in terms of a time argument (noted Teph)
which is close to Barycentric Dynamical Time (TDB), rather than
in terms of TCB, the first integral in Recommendation 2 above
may be computed as
 .
.
Resolution B1.6 IAU 2000 Precession-Nutation
Model
The XXIVth International Astronomical Union General
Assembly,
Recognising
-
that the International Astronomical Union and the
International Union of Geodesy and Geophysics Working Group (IAU-IUGG WG)
on 'Non-rigid Earth Nutation Theory' has met its goals by
| a. establishing new high precision rigid Earth nutation
series, such as (1) SMART97 of Bretagnon et al., 1998, Astron.
Astroph. 329, 329-338; (2) REN2000 of Souchay et al.,
1999, Astron. Astroph. Supl. Ser 135, 111-131; (3) RDAN97
of Roosbeek and Dehant 1999, Celest. Mech. 70, 215-253; |
| b. completing the comparison of new non-rigid Earth transfer
functions for an Earth initially in non-hydrostatic equilibrium, incorporating
mantle anelasticity and a Free Core Nutation period in agreement with observations, |
| c. noting that numerical integration models are not yet
ready to incorporate dissipation in the core, and |
| d. noting the effects of other geophysical and astronomical
phenomena that must be modelled, such as ocean and atmospheric tides, that
need further development; |
-
that, as instructed by IAU Recommendation C1 in 1994,
the International Earth Rotation Service (IERS) will publish in the IERS
Conventions (2000) a precession-nutation model that matches the observations
with a weighted rms of 0.2 milliarcsecond (mas);
-
that semi-analytical geophysical theories of forced
nutation are available which incorporate some or all of the following -
anelasticity and electromagnetic couplings at the core-mantle and inner
core-outer core boundaries, annual atmospheric tide, geodetic nutation,
and ocean tide effects;
-
that ocean tide corrections are necessary at all
nutation frequencies; and
-
that empirical models based on a resonance formula
without further corrections do also exist;
Accepts
the conclusions of the IAU-IUGG WG on Non-rigid
Earth Nutation Theory published by Dehant et al., 1999, Celest.
Mech. 72(4), 245-310 and the recent comparisons between the
various possibilities, and
Recommends
that, beginning on 1 January 2003, the IAU 1976
Precession Model and IAU 1980 Theory of Nutation, be replaced by the precession-nutation
model IAU 2000A (MHB2000, based on the transfer functions of Mathews, Herring
and Buffett, 2000 - submitted to the Journal of Geophysical Research)
for those who need a model at the 0.2 mas level, or its shorter version
IAU 2000B for those who need a model only at the 1 mas level, together
with their associated precession and obliquity rates, and their associated
celestial pole offsets at J2000, to be published in the IERS Conventions
2000, and
Encourages
-
the continuation of theoretical developments of non-rigid
Earth nutation series,
-
the continuation of VLBI observations to increase
the accuracy of the nutation series and the nutation model, and to monitor
the unpredictable free core nutation, and
-
the development of new expressions for precession
consistent with the IAU 2000A model.
Resolution B1.7 Definition of
Celestial Intermediate Pole
The XXIVth International Astronomical Union General
Assembly,
Noting
the need for accurate definition of reference
systems brought about by unprecedented observational precision, and
Recognising
-
the need to specify an axis with respect to which
the Earth?s angle of rotation is defined,
-
that the Celestial Ephemeris Pole (CEP) does not
take account of diurnal and higher frequency variations in the Earth?s
orientation,
Recommends
-
that the Celestial Intermediate Pole (CIP) be the
pole, the motion of which is specified in the Geocentric Celestial Reference
System (GCRS, see Resolution B1.3) by motion of the Tisserand mean axis
of the Earth with periods greater than two days,
-
that the direction of the CIP at J2000.0 be offset
from the direction of the pole of the GCRS in a manner consistent with
the IAU 2000A (see Resolution B1.6) precession-nutation model,
-
that the motion of the CIP in the GCRS be realised
by the IAU 2000 A model for precession and forced nutation for periods
greater than two days plus additional time-dependent corrections provided
by the International Earth Rotation Service (IERS) through appropriate
astro-geodetic observations,
-
that the motion of the CIP in the International Terrestrial
Reference System (ITRS) be provided by the IERS through appropriate astro-geodetic
observations and models including high-frequency variations,
-
that for highest precision, corrections to the models
for the motion of the CIP in the ITRS may be estimated using procedures
specified by the IERS, and
-
that implementation of the CIP be on 1 January 2003.
Notes
The forced nutations with periods less than
two days are included in the model for the motion of the CIP in the ITRS.
The Tisserand mean axis of the Earth corresponds
to the mean surface geographic axis, quoted B axis, in Seidelmann, 1982,
Celest. Mech. 27, 79-106.
As a consequence of this resolution, the Celestial
Ephemeris Pole is no longer necessary.
Resolution B1.8 Definition and
use of Celestial and Terrestrial Ephemeris Origins
The XXIVth International Astronomical Union General
Assembly,
Recognising
-
the need for reference system definitions suitable
for modern realisations of the conventional reference systems and consistent
with observational precision,
-
the need for a rigorous definition of sidereal rotation
of the Earth,
-
the desirability of describing the rotation of the
Earth independently from its orbital motion, and
Noting
that the use of the "non-rotating origin" (Guinot,
1979) on the moving equator fulfills the above conditions and allows for
a definition of UT1 which is insensitive to changes in models for precession
and nutation at the microarcsecond level
Recommends
-
the use of the "non-rotating origin" in the Geocentric
Celestial Reference System ((GCRS) and that this point be designated as
the Celestial Ephemeris Origin (CEO) on the equator of the Celestial Intermediate
Pole (CIP),
-
the use of the "non-rotating origin" in the International
Terrestrial Reference System (ITRS) and that this point be designated as
the Terrestrial Ephemeris Origin (TEO) on the equator of the CIP,
-
that UT1 be linearly proportional to the Earth Rotation
Angle defined as the angle measured along the equator of the CIP between
the unit vectors directed toward the CEO and the TEO,
-
that the transformation between the ITRS and GCRS
be specified by the position of the CIP in the GCRS, the position of the
CIP in the ITRS, and the Earth Rotation Angle,
-
that the International Earth Rotation Service (IERS)
take steps to implement this by 1 January 2003, and
-
that the IERS will continue to provide users with
data and algorithms for the conventional transformations.
Note
The position of the CEO can be computed from
the IAU 2000A model for precession and nutation of the CIP and from the
current values of the offset of the CIP from the pole of the ICRF at J2000.0
using the development provided by Capitaine et al. (2000).
The position of the TEO is only slightly dependent
on polar motion and can be extrapolated as done by Capitaine et al. (2000)
using the IERS data.
The linear relationship between the Earth?s
rotation angle q and UT1 should ensure the
continuity in phase and rate of UT1 with the value obtained by the conventional
relationship between Greenwich Mean Sidereal Time (GMST) and UT1. This
is accomplished by the following relationship:
q (UT1)=2p
(0.7790572732640+1.00273781191135448x(Julian UT1date-2451545.0))
References
Guinot, B., 1979, in D.D. McCarthy and J.D. Pilkington
(eds.), Time and the Earth?s Rotation, D. Reidel Publ. 7-18.
Capitaine, N., Guinot, B. and McCarthy, D.D.,
2000, Astron.Astrophys.,335, 398-405.
Resolution B1.9 Re-definition
of Terrestrial Time TT
The XXIVth International Astronomical Union General
Assembly,
Considering
-
that IAU Resolution A4 (1991) has defined Terrestrial
Time (TT) in its Recommendation 4,
-
that the intricacy and temporal changes inherent
to the definition and realisation of the geoid are a source of uncertainty
in the definition and realisation of TT, which may become, in the near
future, the dominant source of uncertainty in realising TT from atomic
clocks,
Recommends
that TT be a time scale differing from TCG by
a constant rate: dTT/dTCG = 1-LG, where LG
= 6.969290134´ 10-10 is a defining
constant,
Note
LG was defined by the IAU Resolution
A4 (1991) in its Recommendation 4 as equal to UG/c2
where UG is the geopotential at the geoid. LG
is now used as a defining constant.
Resolution B2 Coordinated Universal
Time
The XXIVth International Astronomical Union General
Assembly,
Recognising
-
that the definition of Coordinated Universal Time
(UTC) relies on the astronomical observation of the UT1 time scale in order
to introduce leap seconds,
-
that the unpredictability of leap seconds affects
modern communication and navigation systems,
-
that astronomical observations provide an accurate
estimate of the secular deceleration of the Earth?s rate of rotation,
Recommends
-
that the IAU establish a working group reporting
to Division I at the General Assembly in 2003 to consider the redefinition
of UTC,
-
that this study discuss whether there is a requirement
for leap seconds, the possibility of inserting leap seconds at pre-determined
intervals, and the tolerance limits for UT1-UTC, and
-
that this study be undertaken in cooperation with
the appropriate groups of the International Union of Radio Science (URSI),
the International Telecommunications Union (ITU-R), the International Bureau
for Weights and Measures (BIPM), the International Earth Rotation Service
(IERS), and relevant navigational agencies.
Resolution B3 Safeguarding
the Information in Photographic Observations
The XXIVth International Astronomical Union General
Assembly,
Pursuant of
its Recommendation C13 (1991) of the XXIst General
Assembly to create accessible archives of the large quantities of observational
material collected during the 20th Century and currently stored on photographic
plates,
Recognising
that unless action is taken, this unique historical
record of astronomical phenomena will be lost to future generations of
astronomers,
Considering
the important efforts made by the Working Groups
on (i) Sky Surveys, (ii) Carte du Ciel plates and (iii) Spectroscopic Data
Archives, as well as by the Centre for European Plates recently launched
at the Royal Observatory of Belgium, in locating and cataloguing plates,
in defining the tools needed to safeguard them, and in negotiating the
means to preserve their recorded information in digital form in the public
domain, and
Realising
that the cataloguing, storage and safeguarding
of the photographic plates is an important aspect for the implementation
of the possible future digitisation processes needed for selective media
transfer of high quality data,
Recommends
the transfer of the historic observations onto
modern media by digital techniques, which will provide worldwide access
to the data so as to benefit astronomical research in a way that is well
matched to the tools of the researcher in the future.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]() are
defined in the same way as w and wi but with quantities calculated
in the GCRS with integrals taken over the whole Earth,
are
defined in the same way as w and wi but with quantities calculated
in the GCRS with integrals taken over the whole Earth,
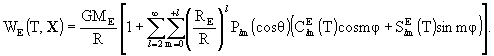
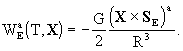
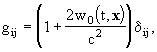
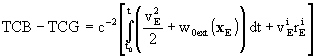
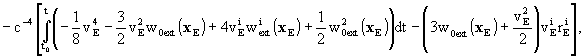
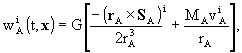
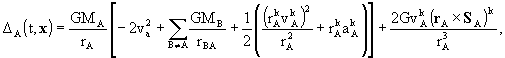
 .
.